On Voting Systems - Almer S. Tigelaar

Voting is simple, right? You just choose a candidate or party and then vote. If everyone does this, the election outcome represents what the majority of people want, and the country gets the leadership that reflects this. At least, that’s the idea. However, voting for one candidate is not without its flaws. What are those flaws and are there better alternatives?

An Unexpected Loss

About twenty years ago, on November 7th 2000 George Bush and Al Gore went head-to-head in the 54th United States presidential elections. However, they were not the only contenders. About six other parties participated in this election. The most well-known are probably Pat Buchanan of the reform party and Ralph Nader of the green party. We’ll get back to Nader later.

The vast majority of the votes went to Bush and Gore. However, it was initially unclear who actually won as networks scrambled to call out the ‘right’ winner first. The process to determine the winner would drag on for weeks due to vote recounts. This close call laid bare a fundamental complication in the American voting system: you can win the popular vote, without winning the overall election. This happened to Al Gore.

The Electoral College

Gore managed to claim 48.38 percent of the popular vote, while Bush got 47.87 percent. However, the way the votes were distributed mattered. The best way to think of this is that each state itself held a ‘local’ popular vote. Whomever won this got all the so-called electoral college votes of that state. The size of the electoral college differs per state, and is relative to that state’s population. Of the 538 electoral votes, Gore won 266 and Bush 271. Thus: Gore won the nationwide popular vote, but lost the sum of all the ‘local’ popular votes.

The same thing happened again sixteen years later. When the republican candidate Trump faced the democratic Hillary Clinton. Like Gore, Clinton won the popular vote with 48.18 percent to Trump’s 46.09 percent. However, she failed to secure the electoral college votes with 227 votes against Trump’s 304. In an ironic twist the 2020 election would see Trump losing with exactly the same difference in electoral college votes to the current president Joe Biden. Although, Biden convincingly won the popular vote with a 4.4 percent lead.

Back to voting in general. You could view this as a problem specific to the American voting system. Wouldn’t a simple solution be to use the nationwide popular vote? Indeed that would have resulted in both the election of Gore (2000) and Clinton (2016). However, it’s still not that simple.

Ranked Voting

Back to one of those alternative candidates in the 2000 elections. Ralph Nader got a full 2.74 percent of the votes. This did not translate into any electoral votes, after all: the states were split between either Gore or Bush. Nevertheless, it reveals a problem inherent to voting for only one candidate.

Consider that many who voted for Ralph Nader, of the Greens, would probably have preferred Al Gore (Democratic) to George Bush (Republican). What if those 2.74 percent would have gone to Gore instead? He would have had 51.2 percent of the popular vote in that case, against Bush’s 47.87 percent. While it’s hard to determine if he would have won, considering the aforementioned electoral college, it’s an interesting idea to entertain. Still there’s an alternative way to look at this and attempt to resolve it.

What if instead of choosing one candidate, the voters would have ranked the candidates from most to least preferred? People preferring Nader and also Gore over Bush would have ranked the candidates as: (1) Nader, (2) Gore and (3) Bush. However, does this really work? For that we travel back to long before this election was ever held: to the eighteenth century.

The Condorcet Paradox

In 1785 Nicolas de Condorcet, a French mathematician, published an essay concerning majority decisions. He posited something we now know as Condorcet’s paradox. Little did he know at the time that Ramon Llull already had discovered this five hundred years earlier. Nevertheless, let’s use the 2000s elections to illustrate this paradox, regardless of its attribution.

We’ll do a radically simplified election. Let’s say there are only three voters that will rank the candidates in order of their preference: Mary, Kenneth and Seth. The table below shows their preference. Observe that Mary prefers Nader first, then prefers Gore over Bush, Kenneth prefers Gore first, but Bush over Nader, etc.

	Mary	Kenneth	Seth
1st	Nader	Gore	Bush
2nd	Gore	Bush	Nader
3rd	Bush	Nader	Gore

This outcome presents us with a problem. The candidates are equally preferred by the first preference of our voters, this is also true for the second and third preference. Perhaps we can now look at which candidate is preferred over which other candidate to resolve this.

So, Mary and Seth prefer Nader over Gore, Mary and Kenneth prefer Gore over Bush, and Kenneth and Seth prefer Bush over Nader. This implies:

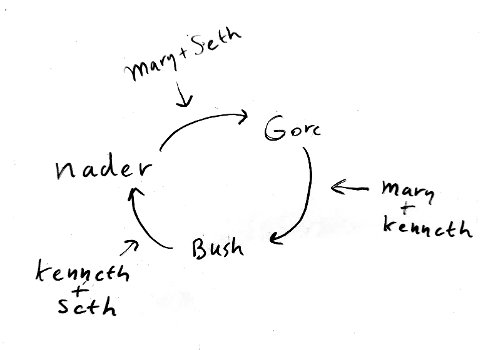
While Nader is preferred over Bush (so it seems), Bush is also preferred over Nader. This is true for any pair of candidates. Hence, we end up in a cycle when we consider the rankings of all voters. Observe that Mary, Kenneth and Seth have no cyclic ambiguity in their own orderings! While at an individual level the preferences are clear, at a collective level there is no clear majority for any candidate. So, while ranked voting can certainly help, and on large populations better captures overall preferences, it can lead to a Condorcet paradox. Can we do better?

Evaluating Ranked Voting Pairs

A simple way to break this paradox is to stop evaluating once we detect a pair (preference of one candidate over another) that leads to a cycle. Following the same order as we did previously, we would get this result, which would lead to Nader being the winner of our simplified ranked election:

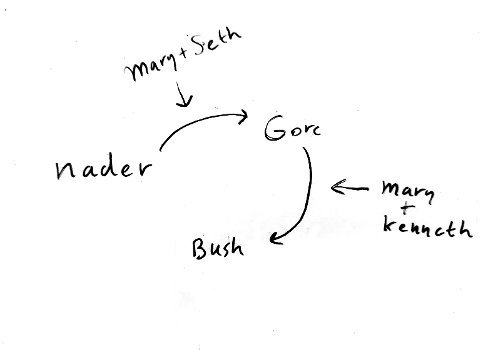
There is a subtlety involved here. Namely, where we start our evaluation (in this case we started with the Nader-Gore pair first), influences where the cycle will be ‘detected’. This can be resolved by deciding on evaluation order beforehand. In a real election we would start with the most commonly occurring adjacent pair in the ranked lists of all voters, which would resolve most of these cases.

Another way to resolve this that may come to mind is to assign points to candidates. For example giving each voters ten points to distribute over all the candidates. This approach was suggested by Jean-Charles de Borda fifteen years prior to his fellow countrymen Condorcet’s writings. However, again Ramon Llull had beat him to it by five hundred years, as was discovered much later.

Borda’s method of distributing points does decrease the probability of cycles occurring, but does not eliminate them entirely. Consider if we gave our voters Mary, Seth and Kenneth six points to distribute, and each would assign three to their first preference, two to the second and one to the third, we’d be back to the exact same Condorcet paradox.

Independence of Irrelevant Alternatives

In our fictive example all the candidates get exactly the same number of votes. This is rarely the case with a large number of voters, even if they would all rank the candidates. This brings us back to the 2000s election and a problem inherent to voting for one candidate and to many vote ranking approaches as well, although with a much lower chance of occurring.

Let’s assume for a moment that everyone who voted for Nader indeed would have preferred Gore over Bush. Thus, if Nader would not have participated his votes would have gone to Gore. We could say that Nader’s presence on the voting ballot ‘spoiled’ the election for Gore. As in: while most people preferred Gore over Bush, Nader participating in the election changed the collective preference, at least at the electoral college level, where the majority went to Bush. All the while individual preferences remained the same: the majority preferred Gore, even though some voted on Nader.

Viewed another way: while Nader had no realistic change of winning, his participation affected the outcome of the election. This effect where the overall outcome does change when we add a seemingly irrelevant third option is referred to as violating independence of irrelevant alternatives. This occurs even in ranked voting, which we saw in the previous section in the form of deciding where to start evaluating pairs. Consider that in the case of ties the presence or absence of a candidate affects the occurrence of a cycle, and thus affects the outcome. Is there a way out of this mess?

Arrow’s Theorem

No, there is not. Condorcet’s paradox as well as the “independence of irrelevant alternatives” are part of a more general theory on social choice. Halfway the twentieth century economist Kenneth Arrow devised his impossibility theorem that states that no rank-order electoral system can be designed that satisfies three fairness criteria if there are more than two candidates:

If every voter prefers candidate A over candidate B, the collective prefers candidate A over candidate B.
If every voter’s preference between candidates A and B remains the same, but changes for other candidates, then the collective preference between A and B remains the same.
No voter has the power to override the overall collective preference.

The first criteria is Condorcet’s paradox. The second is the irrelevance of independent alternatives. The third we have not discussed so far, but seems undesirable in a voting system that aims to reflect the preference of the voting population at large.

Conclusion

Voting is much more complex than seems at first glance. It’s not possible to devise a system that does not suffer from some paradox. A simple fix is having only two candidates to vote for. However, that is hardly realistic in the real world. More realistically trade-offs can be made by choosing certain voting systems over others. Ranked voting systems are in use in various places in the world, for example: Australia, Ireland and Sri Lanka. Despite their flaws, they may better capture electoral preferences. Indeed, it’s usage has been on the rise in the United States more locally.

None of this is to say that trade-offs in voting systems tell us something about the feasibility of say democratic governance. It simply shows that it is mathematically impossible to satisfy all guarantees that we’d perhaps like for an objectively fair election outcome. Even if we intuitively may be led to believe this is trivial. It is not.

Voting for representation with more than two candidates to elect may not be the best approach, but it’s the best we know. It’s likely better served with a form of ranked voting rather than limiting voters to one option.